|
|
The
example with algae is about observations, but works just as well for explanation
models: One can never be sure that a certain model will give the right explanation,
even if it is as the model predicts. There can always exist one or more
models that predict the same explanation. If, to the contrary, what the
model predicts does not correspond with the explanation, we can be sure
that the model is incorrect.
Predictions in an example with mussels
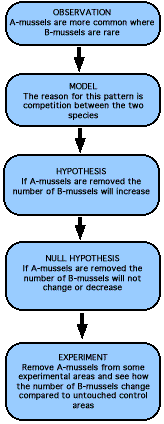 |
In the case of the different species of mussels, the
prediction from the first model is that if the A-mussels are removed
from certain areas there would be no competition and B-mussels
can colonize these areas. They will increase in numbers. In a corresponding
way, if B-musels are removed, A-mussels will increase in number because
of reduced competition.
If any of these predictions are wrong, then the model is
also incorrect. The model states that the distribution of species is
dependent of competition, if competition is removed, distribution
should also change. If distribution does not change, then the reason
for the pattern of distribution cannot be competition.
The other model gives rise to very different predictions:
If the distribution of mussels is dependent of salinity, then A-mussels
would probably die because of the lower salinity if they are removed
from an area where they are common to the area where B-mussels are
common. B-mussels would die in larger numbers than A-mussels if moved
to areas where A-mussels are common. This is ncessary, otherwise
it is not salinity that has affected distribution. |
 |
Page
6 of 13 |
 |
|